Notação Big(O)

Entenda como analisar a performance de algoritmos utilizando a notação Big(O).

A notação Big(O) é uma notação matemática que descreve os limites e comportamentos de um algoritmo para um valor particular ou infinito.

De modo mais simples, ela descreve a complexidade de um código usando termos matemáticos simples de serem compreendidos.

Repare na imagem a seguir um gráfico sobre as suas formas de representação, que serão estudadas a seguir:

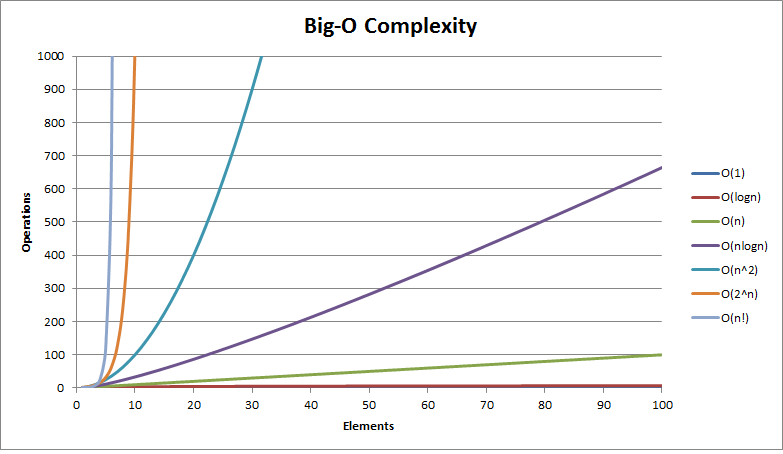
No gráfico acima, a sua direita na legenda, temos os nomes das notações (O(1), O(n),...), nomes estes utilizados para representar a performance de um algoritmo.

Para saber qual o melhor ou pior, devemos olhar para a linha do gráfico, onde a melhor performance será do algoritmo que possuir o menor número de operações (operations) para a maior quantidade de elementos (elements).

Isto faz sentido se pensarmos de modo prático, pois queremos processar o maior número de elementos com a menor quantidade de operações, o que significa que ele será executado mais rapidamente.

Para ficar ainda mais claro o raciocínio, imagine que desejamos ordernar uma lista de números inteiros com 100 elementos. Suponha que tenhamos dois algoritmos, sendo que o primeiro consegue ordenar a lista em 200 operações e o segundo em 500 operações, neste caso fica claro que o primeiro algoritmo finalizará a execução do mesmo em menos da metade do tempo do segundo algoritmo, significando que ele é mais eficiente que o segundo algoritmo.

Agora que você já entendeu a relação entre o número de elementos e operações, verifique novamente o gráfico acima e tente mapear quais notações são mais performáticas e quais são mais lentas.

Entendido o gráfico e sua relação de elementos e operações no impacto de sua execução, vamos agora entender o que causa esse comportamento em nossos algoritmos estudando suas principais notações.

Notação fatorial O(n!)

Fatorial por definição matemática significa o produto de números inteiros positivos de um número natural n maior ou igual a ele.

Para ficar mais simples, vamos a um exemplo básico de cálculo do fatorial de 5, ou 5!, que seria:

5! = 5 * 4 * 3 * 2 * 1 = 120

Se repararmos no cálculo do fatorial de 10, veja como o resultado aumenta significativamente:

10! = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 3628800

Olhando para esses dois resultados, podemos fazer a analogia com a definição da notação fatorial, que é um algoritmo que incrementa sua complexidade com um pequeno aumento no valor de entrada.

Isso faz com que este algoritmo tenha uma performance muito ruim, pois ele somente conseguirá executar um bloco de código para valores pequenos, portanto este é considerado o pior tipo de algoritmo segundo a notação.

Para exemplificar um exemplo de algoritmo nesta notação, nada melhor do que o próprio cálculo do fatorial, conforme demonstrado a seguir:

public int calcularFatorial(int n) {
    if (n == 0) {  
        return 1;    
    } else {
        return(n * calcularFatorial(n-1));
    }
}

Repare que ele faz chamadas recursivas a cada iteração, fazendo com que essas chamadas se incrementem de modo muito rápido a cada incremento de valor na chamada do algoritmo.

Embora este tipo de algoritmo deva ser evitado ao máximo, existem alguns problemas complexos na matemática nos quais somos forçados a utilizar tal solução.

Notações exponenciais O(2^n) e O(n^2)

Algoritmos exponenciais também são de baixa performance e devem ser evitados ao máximo o seu uso.

É muito comum em entrevistas recebermos exercícios onde a solução mais óbvia é utilizar uma solução exponencial, mas caso ela seja utilizada, provavelmente você não terá sucesso na mesma. Devido a isso temos a importância de conhecermos e estudarmos algoritmos a fundo, pois assim saberemos como escrever algoritmos mais eficientes.

Os algoritmos exponenciais tem por característica seu incremento muito rápido, dobrando ou triplicando a quantidade de operações para um simples incremento de valor na entrada.

Normalmente estes algoritmos são caracterizados por dois ou mais laços encadeados, conforme o exemplo a seguir:

void imprimirPares(int lista[]) {
    for (int i = 0; i < lista.length; i++) {
        for (int j = 0; j < lista.length; j++) {
            System.out.println(lista[i] + ", " + lista[j]);
        }
     }
}

Caso você tente simular a execução deste algoritmo, verá que para cada incremento no tamanho da lista, o número de operações se multiplica drasticamente, fazendo com que ele se torne lento para um lista com um tamanho relativamente pequeno.

Notação logarítmica linear O(n * log n)

A notação logarítmica linear já é considerado um algoritmo de performance boa, tanto que um dos mais populares algoritmos de busca, o Merge Sort, que estudaremos em breve, possui esta performance.

A definição de logarítmo na matemática pode parecer um pouco confusa, mas para simplificar basta olharmos para o gráfico logarítmo dela para entender o seu comportamento.

Caso você olhe na imagem acima referênte ao gráfico das complexidades, repare nas linhas onde temos o log (log n e n * log n), e veja como essas linhas não incrementam de modo rápido ao longo do tempo.

Uma função logarítmica cresce de modo lento e constante ao longo do tempo, portanto este tipo de algoritmo mantém uma boa performance mesmo quando usados para processar grandes quantidades de elementos.

Entendido o comportamento do algoritmo logarítmico, repare que este aqui ainda inclui em sua notação a operação n multiplicada pelo log, onde n é a quantidade de elementos da lista de entrada.

Portanto, esta notação seria a combinação da notação linear O(n) com a notação O(log n), que veremos na sequência.

Conforme mencionado anteriormente, um ótimo exemplo para este tipo de algoritmo é o Merge Sort, que devido a sua maior complexidade não colocarei o código aqui, mas ele será estudado em breve neste curso.

Notação linear O(n)

A notação linear, conforme o próprio nome indica, ela demanda mais operações de modo proporcional a quantidade de elementos de entrada.

Um exemplo simples para entender a notação linear, seria um código para imprimir os elementos de uma lista, conforme o exemplo a seguir:

void imprimirLista(int lista[]) {
    for (int i = 0; i < lista.length; i++) {
        System.out.println(lista[i]);
    }
}

Olhando para o código, percebemos que se tivermos uma lista com dez elementos, precisaremos de dez iterações para imprimir os seus valores. Caso tenhamos mil elementos, precisaremos de mil iterações, e assim por diante, sendo que sua performance sempre se mantém linear conforme a entrada de dados.

Algoritmos lineares possuem boa performance, pois eles nunca demandam uma quantidade muito desproporcional de operações para seu processamento quando comparada com a sua entrada de dados.

Notação logarítmica O(log n)

A notação logarítmica indica uma performance muito boa, pois a sua curva diz que o número de operações para realizar um processamento é menor do que a quantidade de elementos de entrada.

Isto significa que ela tem uma performance ainda melhor do que a notação linear, e algoritmos com esta característica são algoritmos bastante eficazes.

Um ótimo exemplo de notação logarítmica é o algoritmo de busca binária, que será estudado mais adiante, pois ele realiza a busca de um elemento em uma lista utilizando divisões na mesma, o que significa que ele não precisa olhar na lista toda para encontrar um valor uma vez que ele vai eliminando metade da lista a cada iteração.

Notação constante O(1)

Por fim temos a notação contante, que significa que independente da quantidade de elementos na entrada, ela sempre necessitará o mesmo número de operações para concluir o processamento do código.

Esses algoritmos são excelentes pois eles sempre terão a mesma performance independentemente da entrada de dados.

No código a seguir temos uma exemplo de notação constante, que imprime o primeiro elemento de uma lista.

void imprimirPrimeiroElemento(int lista[]) {
    System.out.println("Primeiro elemento da lista = " + lista[0]);
}

Repare que ele sempre executará apenas uma operação independentemente do tamanho da lista de entrada, o que significa que ele é bastante eficiente.

Conclusão

Notação Big(O) é um tópico complexo a primeira vista, são muitas informações para serem entendidas ao mesmo tempo, portanto não se preocupe muito caso alguns detalhes não tenham ficado muito claros.

Com o estudo dos algoritmos de busca e ordenação que demonstraremos na sequência, tudo ficará mais claro, pois teremos mais exemplos práticos de análise dos mesmos.

A notação Big(O) é um tópico muito importante em entrevistas, e é muito comum o entrevistador perguntar como você avaliaria a performance de algum algoritmo que tenha criado durante o teste, portanto tenha certeza de estar sempre praticando e entendendo cada vez mais sobre este tópico.